Curriculum Timing for Difficult Math Questions
Imagine picking up a sport for the first time. You may play basketball in the park with some friends or kick a soccer ball around. There is nothing knowledge intensive about shooting a basket or kicking a soccer ball. Majority of the people can perform these actions without the coaching of others fairly easily (though maybe not well).
One day, you feel inspired and impressed by your own abilities. You want to join a league. You decide it is time to take it to the next level on your sports journey. You sign up for your local basketball or soccer league and go to your first game. However, now there is structure ingrained. There are rules and procedures you need to know. Of course, you can still play without knowing all of the rules and procedures, but definitely not as well as someone who does. Not to mention knowing all of the strategic plays and positioning that can put you in the best situations to win the game.
A similar situation arises in our math classrooms every day when we decide the problems to give students. All of our students know how to do math (at least we hope they do). But do the students know they key information in order to play the game properly? Do they know what piece of knowledge they need or are missing in order to solve a problem?
Since many of our students do not do math casually (though that would be very helpful), we need to teach them the knowledge to help them get game ready.
Curriculum Timing
A good curriculum considers the readiness of students to engage in problems. If students do not have the pre-requisite knowledge to solve a problem, they only get frustrated. We cannot solve problems that we do not understand the mathematics behind. For example, consider this problem I pulled from Delta Math.
Now, this is a pretty straight forward question of DOK 1 or 2 (depending whom you are talking to). If you know how to decompose exponents, then the answer comes out through a step by step procedure (split the exponent up into two bases and simplify). However, if you are unfamiliar with decomposing exponents, you’re going to have a rough time. Even if you know exponent properties, many students would not have the intuition of completing them backwards. Hence, there is no “problem solving strategy".
I believe a lot of outsiders (noneducators or influencers) fail to understand that there is a base level of knowledge needed to do mathematics. Many curriculums hail problem solving as king and knowledge is just magically obtained down the road or through problem solving. Emphasizing knowledge attainment is key if we want students to answer more difficult questions (specifically the hard state level test questions).
Which leads me to this point in the article: when are we able to give students the high level questions in class ?
This question requires students to show their work, explain their answer, and provide justification for it. Furthermore, it is a fairly abstract problem students need to solve. Without knowledge of quadratics and coordinate movement, a student would be extremely loss with “problem solving strategies” alone.
Problem Solving is Great, but Knowledge is King
Undoubtedly, knowledge is king. It provides us access into being able to solve difficult problems. Students will never be able to answer the difficult questions we want them to without attaining understanding AND fluency in the content first. Once students gain both of these, then we can begin talking about answering difficult questions.
I recommend that you plan your units in the following way.
Begin by teaching students the content with direct instruction. It gets them the information quickly and allows them to begin building fluency
Give regular quizzes to assess students knowledge and group units into sections of similar content
At the end of the Unit, begin introducing the more difficult abstract questions to students. Have them attempt the problem, then review the problem on the board with them (reverse instruction)
End the Unit with an exam that includes all types of questions (including the open ended ones!!)
In general, most math units are planned out this way, but some curriculum providers believe they are recreating the wheel with their approaches. You can also integrate more open ended questions through out the unit if you would like, however I find that leaving them towards the end allows students to be more successful when preparing for the exam.
And for whatever method, style, or learning approach you take, I guarantee this: students will always be more successful when they have the appropriate knowledge to address a problem. Otherwise, you are wasting your time.


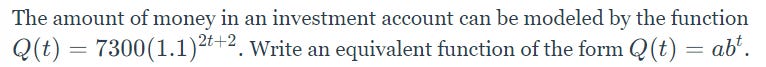


I enjoy reading your pieces. Please keep them coming!
I think this works very well for some units and not so well for others. For example, I take a similar approach to Systems of equations with my 8th grade Algebra class: we intro systems, learn the different ways to solve them and then finally I introduce real world problems.